Selbstabschirmung ist ein wesentlicher Aspekt Reaktionsraten der Berechnung, die sehr starke Auswirkungen auf zahlreiche Observablen von Kritikalität Aktivierung haben. Es gibt zwei allgemeine Arten von Selbstabschirmung, die als Energie und räumliche Selbstabschirmung oft klassifiziert sind. Methoden für die dieser selbstschütz Fragen für beide Reaktionsraten zu korrigieren haben innerhalb FISPACT-II umgesetzt.
Das wesentliche Merkmal des Energieselbst Abschirmung besteht darin, dass Querschnitte oft Resonanzen enthalten, die für ganz bestimmte Energiebereiche definiert, die oft große Beiträge zu der Gesamtreaktionsrate aufweisen. Die große Resonanz wird eine Vertiefung in der Neutronenpopulation führen um diese Energie, die möglicherweise nicht in der Simulation zu berücksichtigen, sofern diese Rückkopplung nicht in vollem Umfang berücksichtigt. Es ist besonders problematisch, wo Querschnitte und Partikelspektren in eine Mehrgruppen diskretisiert werden, wo die Vertiefung in der Population für eine bestimmte Energie nicht aufgelöst werden kann.
Räumliche Selbst Abschirmung befasst sich mit der Tatsache, dass Neutronenflusses und lokale Spektren deutlich über kurze Strecken geändert werden. In Fällen mit starken Resonanzen kann die Veränderung in der Partikelspektrum über kurze Entfernungen sehr groß in der Region um die Resonanz.
Energie-abhängige Selbstabschirmung
FISPACT-II beschäftigt Wahrscheinlichkeitstabellen erzeugt durch CALENDF-2010 Material und Verdünnungsraten spezifische Reaktion zu bieten. Wahrscheinlichkeitstabellen für Makroteilquerschnitte einschließlich der elastischen Streuung, Absorption, Spaltung, unelastische Streuung und Neutronenproduktion (ohne Spaltung) zur Verfügung gestellt. Eine unendliche Verdünnung Querschnitt beruht auf der Rohspektrum und Querschnitte errechnet, die in Gauss erweitert werden kann Quadraturen:
$$\sigma(x,d=\infty) = \frac{1}{E_{max}-E_{min}}\int_{E_{min}}^{E_{max}} \sigma(E)\, dE = \sum_{n=1}^N P(x,n) \sigma(x,n). $$
Die Querschnitte $ \ sigma $ und Wahrscheinlichkeitstabellen $ P $ sind abhängig von der Mutter-Nuklid $ p $, $ g $ Energie Gruppe, Makro-Teilindex $ x $ und Quadratur-Index $ n $. Wenn ein Nuklid Bestandteil einer homogenen Mischung ist, werden die effektiven Querschnitte in den Resonanzbereichen reduziert und parametriert werden können die Verdünnung:
$$\sigma(x,d) =\frac{\sum_{n=1}^N P(x,n) \sigma(x,n)/(\sigma_{t}(n)+d)}
{\sum_{n=1}^N P(x,n) /(\sigma_{t}(n)+d)} . $$
Verdünnungen werden auf der Grundlage der Materialzusammensetzung und einem iterativen Algorithmus unter Verwendung der Bibliothek Querschnittswerte berechnet. Diese Verdünnungen werden verwendet, um die Querschnitte für die einzelnen Makroteil neu zu berechnen. Zwei verschiedene Ansätze, die durch das PROBTABLE Schlüsselwort zur Verfügung stehen, sind die Reaktionsgeschwindigkeiten Basis don der Gesamtquerschnitt oder Makro partials maßstäblich, die auch unterschiedliche Verdünnungs Algorithmen initiiert. Weitere Informationen finden Sie in Anhang A.4.3 der Bedienungsanleitung.
Die selbstschütz Faktoren werden durch die Verwendung von entweder SSFFUEL angewendet (die nur als Brennstoff Schlüsselwort Isotopen Definitionen verwendet) oder SSFMASS (die durch Massen-% natürliche Elemente verwendet). Spezifische Verdünnungswerte können von Hand mit dem SSFDILUTION Schlüsselwort überschrieben. Weitere Details über die Verwendung dieser Funktionalitäten kann in den Eingängen Abschnitt des Handbuchs zu finden.
Geometrie Selbstabschirmung
FISPACT-II ist ein Punkt-Lösung Code, der nicht direkt die Geometrie eines simulierten Szenario betrachten, sondern mehrere robuste Systematik existieren für die Behandlung von Geometrie Effekte wie Punkt-Source-Dosen und räumliche Selbstabschirmung. Das Schlüsselwort SSFGEOMETRY ermöglicht es dem Benutzer, die „Universal-Kurvenmodell“ zu verwenden, die für Folien, Drähte, Kugeln und Zylindern gezeigt wurde, für die räumliche Selbstabschirmungseffekte eine gute Übereinstimmung zu geben. Dies betrachten wir eine Resonanz in einem reinen Ziel, eine universelle dimensionsloser Parameter verwenden,
$$ z = \Sigma_{tot}(E_{res}) L_{eff} \sqrt{\frac{\Gamma_\gamma}{\Gamma}}, $$
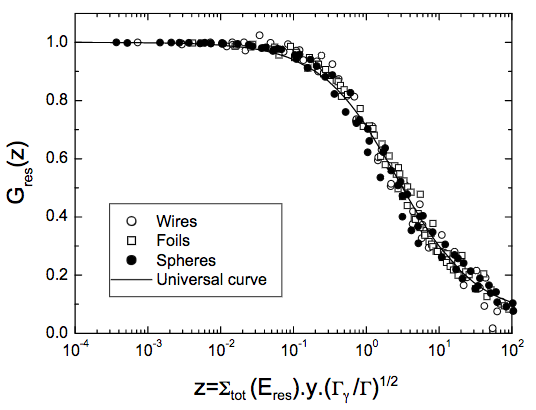
Universal-Kurve der Resonanzselbstabschirmung Faktoren gegen $ z $ Werte für Drähte, Folien und Kugelgeometrien zeigt. Genommen von E. Martinho et al.
based on macroscopic cross section at the energy of the resonance $\Sigma_{tot}(E_{res})$, ‚effective length‘ $L_{eff}$, radiative capture width $\Gamma_\gamma$ and total resonance width $\Gamma$. The seld-shielding factor for this resonance is then a function only of $z$ with empirical constants.
basierend auf makroskopischen Querschnitt bei der Energie der Resonanz $ \ sigma_{tot} (E_{res}) $ „effektive Länge“ $ L_{eff} $, Breite Strahlungseinfang $ \Gamma_\gamma $ und Gesamtresonanzbreite $ \Gamma $. Die selbstschützFaktor für diese Resonanz ist dann nur eine Funktion von $ z $ mit empirischen Konstanten.
Das Modell wurde an eine Gruppe von getrennten Resonanzen verlängert durch eine gewichtete Summe der selbstschützenden Faktoren mit Gewichten unter
$$w_i = \left( \frac{\Gamma_\gamma \Gamma_n}{E^2_{res} \Gamma} \times \frac{2J+1}{2(2I+1)} \right)_i , $$
wobei $ \ Gamma_n $ die Neutronenstreuung Breite, I $ $ und $ J $ sind die Spins der Ziel und Verbindung Resonanzzustände sind. FISPACT-II kann diese auf einer Gruppe-by-Gruppenbasis für alle Nuklide innerhalb des Targetmaterials zu verwenden, um die Abschirmung Faktoren für alle Querschnitte selbst bietet das Stichwort PRINTLIB verwenden.
