Auto-protection est un aspect essentiel du calcul des vitesses de réaction qui peuvent avoir des effets très importants sur de nombreux observables de criticité à l’activation. Il existe deux types généraux de l’auto-protection qui sont souvent classés comme l’énergie et l’espace libre blindage. Méthodes de correction des vitesses de réaction pour ces deux questions d’auto-protection ont été mises en œuvre au sein de FISPACT-II.
La caractéristique essentielle de l’énergie auto blindage est que des sections contiennent souvent des résonances qui sont définies pour les régions très spécifiques de l’énergie, qui ont souvent de grandes contributions pour la vitesse de réaction totale. La grande résonance provoque une dépression dans la population de neutrons autour de cette énergie qui ne peut être reflétée dans les simulations où ces commentaires ne sont pas pleinement pris en compte. Il est particulièrement problématique lorsque des sections transversales et des spectres de particules sont discrétisées dans certains multi-groupe où la dépression dans la population pour une énergie spécifique ne peut être résolu.
Spatiales offres de autoprotection avec le fait que le flux de neutrons et les spectres locaux peuvent être modifiés de manière significative sur de courtes distances. Dans les cas de fortes résonances, le changement dans le spectre de particules sur de courtes distances peut être très importante dans la région autour de la résonance.
Énergie dépendante auto blindage
FISPACT-II emploie des tables de probabilités générées par CALENDF-2010 pour offrir du matériel et de dilution des vitesses de réaction spécifiques. des tables de probabilités sont prévus pour des sections transversales partielles, y compris des macro-diffusion élastique, l’absorption, la fission, la diffusion inélastique des neutrons et la production (à l’exclusion de fission). Une section transversale dilution infinie est calculée sur la base du spectre brut et des sections, qui peut être agrandi en Gauss Quadratures:
$$\sigma(x,d=\infty) = \frac{1}{E_{max}-E_{min}}\int_{E_{min}}^{E_{max}} \sigma(E)\, dE = \sum_{n=1}^N P(x,n) \sigma(x,n). $$
Les croisées sections $ \sigma $ et des tables de probabilité $ P $ dépendent du parent nucléide $ p $, l’énergie groupe $ g $, macro-index partielle $ x $ et l’indice de quadrature $ n $. Quand un nucléide est un constituant d’un mélange homogène, les sections transversales efficaces des régions de résonance sont réduites et peuvent être paramétrées en utilisant la dilution:
$$\sigma(x,d) =\frac{\sum_{n=1}^N P(x,n) \sigma(x,n)/(\sigma_{t}(n)+d)}
{\sum_{n=1}^N P(x,n) /(\sigma_{t}(n)+d)} . $$
Les dilutions sont calculées en fonction de la composition du matériau et un algorithme itératif en utilisant les valeurs de la section bibliothèque de croix. Ces dilutions sont utilisées pour recalculer les sections pour chaque macro-partiel. Deux approches différentes qui sont disponibles à travers le mot-clé PROBTABLE, sont à l’échelle de la base de taux de réaction don total section ou macro-partials, qui initie également des algorithmes différents de dilution. Pour plus de détails voir l’annexe A.4.3 du manuel d’utilisation.
Les coefficients d’auto-protection sont appliquées par l’utilisation de l’une SSFFUEL (qui utilise les définitions des isotopes comme le mot-clé FUEL) ou SSFMASS (qui utilise des éléments naturels en% en masse). Les valeurs de dilution spécifiques peuvent être écrasées par la main en utilisant le mot-clé SSFDILUTION. Plus de détails sur l’utilisation de ces fonctionnalités peuvent être trouvées dans la section des entrées du manuel.
Géométrie auto blindage
FISPACT-II est un code de point solution qui ne considère pas directement la géométrie d’un scénario simulé, mais plusieurs Systématique robustes existent pour le traitement des effets de géométrie tels que les doses de source ponctuelle et spatiale auto blindage. Le mot-clé SSFGEOMETRY permet à l’utilisateur d’employer le «modèle de courbe universelle » qui a été démontré pour les feuilles, des fils, des sphères et des cylindres pour donner un bon accord pour les effets spatiaux auto de blindage. Ceux-ci considèrent une résonance dans une cible pure, en utilisant un paramètre sans dimension universelle,
$$ z = \Sigma_{tot}(E_{res}) L_{eff} \sqrt{\frac{\Gamma_\gamma}{\Gamma}}, $$
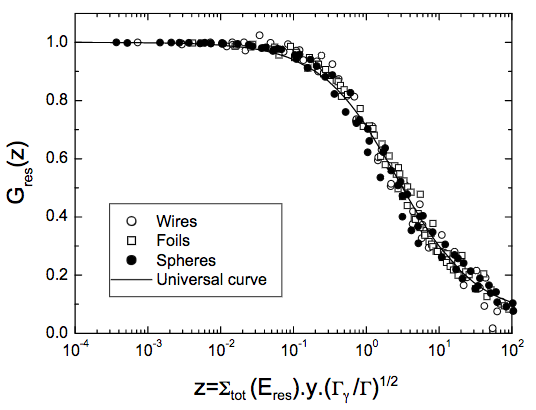
Courbe universelle des résonance facteurs auto de blindage contre $ z $ montrant des valeurs pour des fils, des feuilles et des géométries de sphère. Tiré de E. Martinho et al.
sur la base de section transversale macroscopique à l’énergie de la résonance $ \sigma_{tot} (E_{res})$, longueur effective $ L_{eff} $, capture radiative largeur $ \Gamma_\gamma $ et la résonance largeur totale $ \Gamma $. Le facteur d’auto-blindage pour cette résonance est alors une fonction seulement de $ z $ avec des constantes empiriques.
Le modèle a été étendue à un groupe de résonances séparées en prenant une somme pondérée des coefficients d’auto-protection avec des poids
$$w_i = \left( \frac{\Gamma_\gamma \Gamma_n}{E^2_{res} \Gamma} \times \frac{2J+1}{2(2I+1)} \right)_i , $$
où $ \Gamma_n $ est la largeur de la diffusion des neutrons, $ I $ et $ J $ sont les spins des cibles et de résonance composé états, respectivement. FISPACT-II peut utiliser ceux-ci sur une base groupe par groupe pour tous les nucléides dans le matériau cible, en fournissant les facteurs auto de blindage pour toutes les sections en utilisant le mot-clé PRINTLIB.
