Getting started: reactor power simulation
As an alternative to the use of FLUX to determine reaction rates, the user may employ the POWER keyword with a volumetric power and the kerma mt number(s) responsible for the heat. In most cases this should be the total kerma value mt=301. Note that the POWER keyword may only be used for those libraries containing the relevant kerma cross-section data.
A set of example cases have been put in the reactor power folder of getting_started. The fluxes file contains an example PWR spectrum and the files file is similar to those from the ssion pulse examples with the exception of the temperature-dependence of the cross sections, which is given by:
# Library cross section data xs_endf ../../ENDFdata/TENDL2014data/tal2014-n/gxs-709-600
The temperature is given in the last three characters - in this case 600 K. Now open the 150Wcc_1.i input which contains several familiar lines, but with FLUX replaced by POWER:
POWER 150.0 1 301 ATOMS << -----irradiation phase----- >> TIME 1 YEARS ATOMS << -----cooling phase----- >>
POWER comes in this case with three arguments which are the volumetric power of 150 W cm\(^{-3}\), the number of channels and total kerma mt. This input will simulate a one year irradiation at this power density, but without any reaction rate updates. In reality, reaction rates vary during operation and must be renormalised with some regularity. To update the reaction rates, we can add additional POWER keywords, for example in 150Wcc_2.i:
POWER 150.0 1 301 ATOMS << -----irradiation phase----- >> TIME 0.5 YEARS ATOMS POWER 150.0 1 301 TIME 0.5 YEARS ATOMS << -----cooling phase----- >>
This amounts to a renormalisation every 6 months. There are a total of eight simulation inputs labelled as </tt>150Wcc_X.i</tt>, where X is the number of updates per year. Run FISPACT-II with the fisprun script and you should see the messages:
Running collapse/condense with TENDL-2014 709-xs, ENDF/B-VII.1 nFY+DD collapse: cpu time = 40.5 secs. 2 errors/warnings, for details see runlog condense: cpu time = 1.59 secs. 76 errors/warnings, for details see runlog Running 150 W/cm3 with varying POWER updates 150Wcc_1: cpu time = 2.03 secs. No errors/warnings 150Wcc_2: cpu time = 2.23 secs. No errors/warnings 150Wcc_4: cpu time = 2.50 secs. No errors/warnings 150Wcc_12:cpu time = 3.83 secs. No errors/warnings 150Wcc_26:cpu time = 5.82 secs. No errors/warnings 150Wcc_52:cpu time = 10.0 secs. No errors/warnings 150Wcc_183cpu time = 28.0 secs. No errors/warnings 150Wcc_365cpu time = 53.1 secs. No errors/warnings Running various W/cm3 simulations with 1 week POWER updates 50Wcc_52: cpu time = 9.63 secs. No errors/warnings 60Wcc_52: cpu time = 9.32 secs. No errors/warnings 80Wcc_52: cpu time = 9.80 secs. No errors/warnings 100Wcc_52:cpu time = 9.91 secs. No errors/warnings 125Wcc_52:cpu time = 9.89 secs. No errors/warnings 150Wcc_52:cpu time = 9.95 secs. No errors/warnings 200Wcc_52:cpu time = 10.2 secs. No errors/warnings 250Wcc_52:cpu time = 10.3 secs. No errors/warnings 300Wcc_52:cpu time = 10.0 secs. No errors/warnings
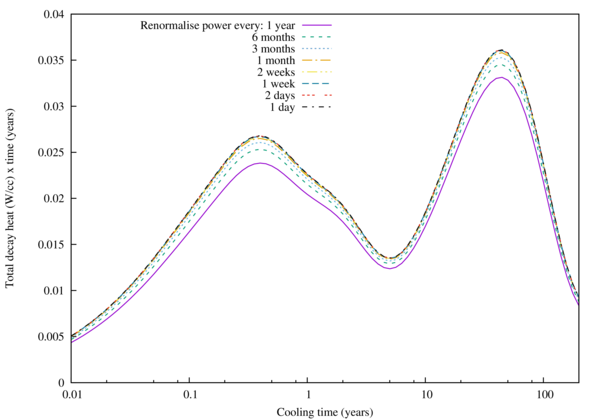
Note that this script also performs the simulations for the next study in this example. Each of the 150 W cm\(^{-3}\) simulations will produce a .gra file which can be plotted with the vary re-simulate.plt gnuplot script in the plot/ folder. This should generate the plot shown in figure to right. The y-axis is the volumetric decay power times the cooling time, which provides more visually discernible patterns. The rst `bump' is due to several nuclides with Zr95 the most dominant. The second peak is due to Cs137 and Sr90. The simulation without any reaction rate updates can under-estimate by nearly 20% and convergence is adequately reached with approximately 2 week intervals between renormalisations.
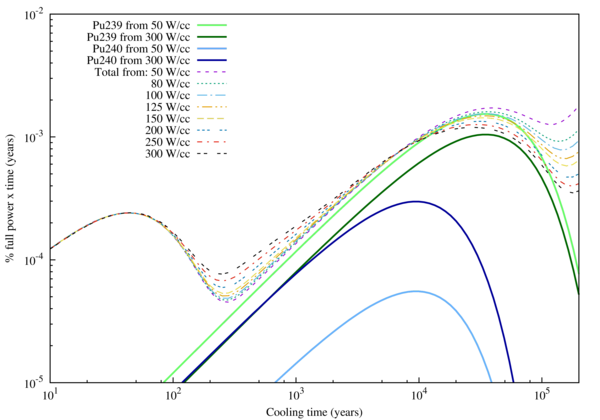
Now lets consider the other inputs which were run with fisprun. These include several diffrent volumetric power simulations with the same 1 week between power renormalisations, making this error negligible. The di erent power densities equate to different burn-up values for the same fuel. To compare the results for each simulation with different ssion rates and power outputs, we should examine the % of full power after shut-down, which we multiply by time to obtain the data of figure below. The plotting script to generate this gure is provided in the plot/ folder. In cooling times less than 100 years the % of full power heat is approximately equal between simulations, as we can see in the Cs137/Sr90 peak. However, the plutonium composition is expected to vary depending on the burn-up of the fuel. To demonstrate the di erence, partial heat curves for the dominant plutonium isotopes are shown for the two extreme values of 50 and 300 W cm\(^{-3}\). The lower burn-up results in a higher relative Pu239 concentration and lower Pu240, which gives a lower decay heat between 100-2000 years and a higher heat after 10,000 years.
While these are not physically complete simulations with full irradiation history, density, initial inventory, etc inputs, this simple example demonstrates the code capabilities and with complete input data a user may easily probe inventory and observable quantities.