Getting started: solver convergence
It is important to note that FISPACT-II uses the iterative stiff-ode solver LSODES. Default tolerances for the solver give good accuracy for the numbers of atoms of the major constituents of the inventory, but may give poor results for minor constituents. This may lead to inaccurate predictions of radiological quantities when minor constituents are dominant in radiological activity.
It is good practice to repeat some calculations using tighter tolerances (using the TOLERANCE keyword) to establish that the inventory is calculated accurately enough for relevant radiological outputs to have converged. If the ? flag is set in the inventory table output for nuclides that appear in the dominant nuclide table, then radiological predictions should be treated with caution until convergence studies have been performed.
An example which illustrates this is provided in the tolerance_test/ folder within getting_started/. To underline the importance of solver tolerances, we simulate the nickel foil irradiation performed at the Frascati Neutron Generator facility which has been re-analysed using FISPACT-II. A high-purity foil was irradiated for 10 minutes with a D-T generator, producing approximately 6.0E+08 n cm\(^{-2}\) s\(^{-1}\). The folder contains the standard collapse.i, condense.i, files, fluxes and print_lib.i files, as well as several copies of the same inventory simulation which are labelled ni_X_Y.i, where X and Y refer to the absolute and relative tolerance settings employed by the LSODES solver. To manually edit the tolerance settings in the simulation, the TOLERANCE keyword is added:
<< -----tolerance settings----- >> TOLERANCE 0 1.0E+00 1.0E-07
where these values appear in the ni_1E0_1E-7.i simulation. The fisprun script will run all of the inputs in order and return:
Simulation of FNG nickel foil irradiation using TENDL-2014 collapse: cpu time = 42.9 secs. 2 errors/warnings, for details see runlog condense: cpu time = 8.79 secs. 1 error/warning, for details see runlog print_lib:cpu time = 1.25 secs. No errors/warnings Running over TOLERANCE settings: atol=1E+4 rtol=1E-3 ni_1E4_1E-cpu time = 1.74 secs. No errors/warnings atol=1E+3 rtol=1E-4 ni_1E3_1E-cpu time = 1.62 secs. No errors/warnings atol=1E+2 rtol=1E-5 ni_1E2_1E-cpu time = 1.57 secs. No errors/warnings atol=1E+1 rtol=1E-6 ni_1E1_1E-cpu time = 1.87 secs. No errors/warnings atol=1E+0 rtol=1E-7 ni_1E0_1E-cpu time = 1.92 secs. No errors/warnings atol=1E-1 rtol=1E-8 ni_1E-1_1Ecpu time = 1.70 secs. No errors/warnings atol=1E-2 rtol=1E-9 ni_1E-2_1Ecpu time = 1.67 secs. No errors/warnings
Each of the ni_X_Y.gra outputs contains a summary of the total decay heat, which can be visualised using the plotting script in the plot/ folder:
gnuplot tolerance_test.plt
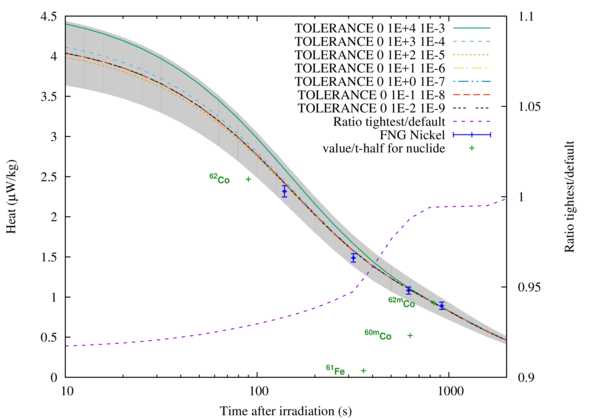
generating tolerance_test.eps which is shown in the figure below. Note that the collapse and condense is the same for all simulations - i.e. all cross sections and decay constants are identical. The only difference is in the numerical solver settings. This gure shows all of the decay heat curves labelled by their tolerance settings, as well as the ratio between the tightest and default tolerance results. The experimental results from FNG are also presented. Note that all simulations and the experimental values lie within the uncertainty due to the nuclear reaction data around the fully-converged result.
The solver uctuation around 10 seconds after irradiation can be traced directly to differences in nuclide inventories which are provided in the FISPACT-II output files. Within the ni_1E-2_1E-9.out file search for the output from the first cooling time at ELAPSED TIME IS 10.000 s. Underneath the DOMINANT NUCLIDES heading are the dominant nuclides for various responses including activity, total heat etc. In this output we find:
NUCLIDE ACTIVITY PERCENT NUCLIDE HEAT PERCENT NUCLIDE
(Bq) ACTIVITY (kW) HEAT
Total 4.0604E+03 Total 2.4877E-13 Total
1 Co 60m 3.1721E+03 78.12E+00 Co 62 1.4080E-13 56.60E+00 Co 62
2 Co 58m 4.4542E+02 10.97E+00 Co 62m 5.6563E-14 22.74E+00 Co 62m
3 Co 62 2.7123E+02 66.80E-01 Co 60m 3.1752E-14 12.76E+00 Ni 57
4 Co 62m 9.5179E+01 23.44E-01 Ni 57 9.6207E-15 38.67E-01 Fe 61
5 Co 61 2.8820E+01 70.98E-02 Fe 61 5.0350E-15 20.24E-01 Co 60m
and when searching for the same data within ni_1E4_1E-3.out we find:
NUCLIDE ACTIVITY PERCENT NUCLIDE HEAT PERCENT NUCLIDE
(Bq) ACTIVITY (kW) HEAT
Total 4.1331E+03 Total 2.7119E-13 Total
1 Co 60m 3.2022E+03 77.48E+00 Co 62 1.6249E-13 59.92E+00 Co 62
2 Co 58m 4.4535E+02 10.78E+00 Co 62m 5.6818E-14 20.95E+00 Co 62m
3 Co 62 3.1302E+02 75.74E-01 Co 60m 3.2053E-14 11.82E+00 Ni 57
4 Co 62m 9.5609E+01 23.13E-01 Ni 57 9.6203E-15 35.48E-01 Fe 61
5 Co 61 2.8776E+01 69.62E-02 Fe 61 5.1868E-15 19.13E-01 Co 60m
While there are some small differences in other nuclides, the Co62 heat value is responsible for the majority of the discrepancy. The output for each time begins with a complete nuclide inventory, which shows the number of atoms for each nuclide. In this simulation with approximately 6.0E+20 atoms, the number of Co62 atoms 10 s after irradiation in the ni_1E4_1E-3 and ni_1E-2_1E-9 simulations are 4.06E+4 and 3.52E+4, respectively. Co62 gives off an average of 3.24 MeV per decay with a half-life of 9 seconds, making these relatively few atoms particularly potent around this cooling time.
In order to avoid solver convergence issues of this kind, is it strongly recommended that users verify convergence or use stricter tolerance settings. For this simulation the cpu cost is not detectable but in more complex simulations with many nuclides such strict tolerances may give some slow-down. However, those are precisely the simulations where relatively small inventory contributions are likely to influence results. While it is uncommon to find such challenging simulations, it is generally easier to guarantee convergence with tight tolerances than to vigilantly verify convergence through tolerance studies.