自屏蔽计算,可以有无数从观测到临界激活很强的影响反应速率的一个重要方面。一般有两种类型的自屏蔽的这往往列为能量和空间自屏蔽。用于校正的反应速率为这两种自屏蔽的问题的方法已经FISPACT-II内实现。
能量自屏蔽的基本特征是,横截面通常包含被用于非常特定的能量的区域,这往往具有朝向总反应速率大的贡献限定共振。大共振会导致周围的能量,可能不会反映在模拟的地方这种反馈是不充分考虑到中子人口萧条。其中,横截面与粒子光谱离散化成一些多组,其中在群体的特定能量的凹陷不能解析它是特别成问题的。
同的事实,中子通量和本地光谱可以在短距离内进行显著改变空间自屏蔽的交易。在具有较强的共振的情况下,在短距离的粒子谱的变化可以是在周围的谐振区域非常大。
能源依赖的自屏蔽
FISPACT-II采用了由CALENDF-2010产生提供材料和稀释的具体反应速率概率表。提供了用于宏观部分横截面,包括弹性散射,吸收,裂变,非弹性散射和中子产生(不包括核裂变)概率表。无限稀释剖面是基于原始谱和横截面,其可在高斯扩展求积计算:
$$\sigma(x,d=\infty) = \frac{1}{E_{max}-E_{min}}\int_{E_{min}}^{E_{max}} \sigma(E)\, dE = \sum_{n=1}^N P(x,n) \sigma(x,n). $$
截面$ \sigma $六西格玛和概率表$ P $取决于母核素$ p $,能源集团$ g $,宏观部分索引$ x $和正交指数$ n $。当一个核素是均相混合物的构成成分,在共振区域中的有效横截面被减小,并且可以使用稀释进行参数:
$$\sigma(x,d) =\frac{\sum_{n=1}^N P(x,n) \sigma(x,n)/(\sigma_{t}(n)+d)}
{\sum_{n=1}^N P(x,n) /(\sigma_{t}(n)+d)} . $$
稀释基于所述材料组合物以及使用该库截面值迭代算法计算。这些稀释液被用来重新计算每个宏局部的横截面。两种不同的方法其可通过PROBTABLE关键字,是按比例的反应速率基不要总截面或宏观的partials,这还启动不同稀释算法。欲了解更多详情,请参阅用户手册的附录A.4.3。
自屏蔽的因素通过使用任一SSFFUEL(使用同位素定义只是作为燃料关键字)或SSFMASS(其以质量%采用自然元素)的应用。特定的稀释值可以手工使用SSFDILUTION关键字被覆盖。关于如何使用这些功能的更多详细信息可在手册的输入部分。
几何自屏蔽
FISPACT-II是一个点溶液代码不直接考虑的模拟场景的几何形状,但对于几何效果,例如点源的剂量和空间自屏蔽的治疗存在若干健壮系统学。关键字SSFGEOMETRY允许用户使用它已被证明为箔,电线,球体和圆柱体,得到用于空间自屏蔽效果好的协议“通用曲线模型”。这些考虑的共振纯目标,使用通用的无量纲参数,
$$ z = \Sigma_{tot}(E_{res}) L_{eff} \sqrt{\frac{\Gamma_\gamma}{\Gamma}}, $$
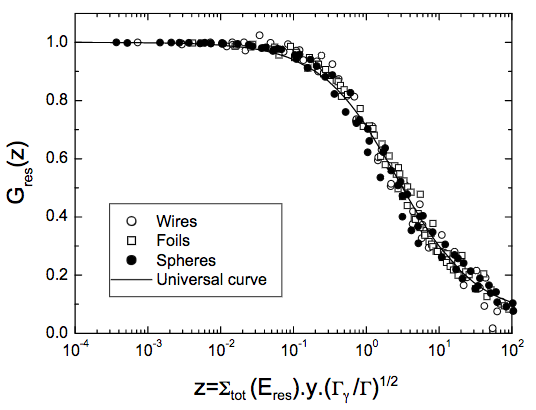
共振自屏蔽因素对$ z $显示了电线,箔和球几何值的通用曲线。来自E. Martinho et al.服用。
based on macroscopic cross section at the energy of the resonance $\Sigma_{tot}(E_{res})$, ‘effective length’ $L_{eff}$, radiative capture width $\Gamma_\gamma$ and total resonance width $\Gamma$. The seld-shielding factor for this resonance is then a function only of $z$ with empirical constants.
基于宏观截面在谐振$ \sigma_{tot}(E_{res})$的能量,“有效长度’$ L_{eff} $,辐射捕获宽度$ \Gamma_\gamma$,总共振宽度$ \Gamma $伽马。对于这种共振自屏蔽系数是那么只有与经验常数$ z $的功能。
该模型已通过取自屏蔽因素的加权和与重量延伸到一组分离的共振
$$w_i = \left( \frac{\Gamma_\gamma \Gamma_n}{E^2_{res} \Gamma} \times \frac{2J+1}{2(2I+1)} \right)_i , $$
其中$ \Gamma_n $ 是中子散射宽度,$ I $和附加$ J $是目标和复合共振态的自旋,分别为。 FISPACT-II可以在一组逐个组的基础为目标材料之内的所有核素使用这些,提供自屏蔽因素使用PRINTLIB关键字的所有横截面。
