自己遮蔽は活性化に重要性から多数の観測に非常に強力な効果を持つことができる反応速度を計算する重要な側面です。多くの場合、エネルギーと空間自己シールドとして分類されている自己シールドの2つの一般的なタイプがあります。これらの自己遮蔽の問題の両方に反応速度を補正するための方法はFISPACT-II内に実装されています。
エネルギー自己遮蔽の本質的な特徴は、断面は、多くの場合、多くの場合、総反応速度に向けて大きな貢献を持っている非常に特定のエネルギー領域、のために定義されている共鳴を含むことです。大きな共鳴は、このフィードバックが十分に考慮されていないシミュレーションに反映されない場合があり、そのエネルギーの周りの中性子の集団におけるうつ病の原因となります。断面と粒子スペクトルは、特定のエネルギーのための母集団におけるうつ病は解決できない一部のマルチグループに離散化されている場合には特に問題となります。
中性子束及びローカルスペクトルは有意に短い距離にわたって変化させることができるという事実と空間自己遮蔽扱います。強い共鳴との例では、短距離粒子スペクトルの変化は、共振の周辺地域の非常に大きくなることがあります。
エネルギー依存性の自己シールド
FISPACT-IIは、材料および希釈特定の反応速度を提供するためにCALENDF-2010によって生成される確率テーブルを採用しています。確率テーブルは、弾性散乱、吸収、分裂、非弾性散乱中性子生産(分裂を除く)を含むマクロ部分断面のために提供されます。無限希釈断面がガウス求積法で展開することができる生のスペクトルと断面に基づいて計算されます。
$$\sigma(x,d=\infty) = \frac{1}{E_{max}-E_{min}}\int_{E_{min}}^{E_{max}} \sigma(E)\, dE = \sum_{n=1}^N P(x,n) \sigma(x,n). $$
断面$ \シグマ$と確率テーブル$ P $は、親核種$ p $、エネルギーグループのグラムの$ g $、マクロ部分インデックスの$ x $と直交インデックスの$ n $に依存しています。核種は、均一な混合物の成分である場合には、共振領域内の有効断面積が低減され、希釈を使用してパラメータ化することができます。
$$\sigma(x,d) =\frac{\sum_{n=1}^N P(x,n) \sigma(x,n)/(\sigma_{t}(n)+d)}
{\sum_{n=1}^N P(x,n) /(\sigma_{t}(n)+d)} . $$
希釈は、材料組成およびライブラリ断面値を用いて反復アルゴリズムに基づいて計算されます。これらの希釈液を各マクロ部分のための断面を再計算するために使用されます。 PROBTABLEキーワードを介して使用できる2つの異なるアプローチは、反応速度ベースドンをスケーリングするためにある全断面積または異なる希釈アルゴリズムを開始するマクロパーシャル、。詳細についてはユーザーマニュアルの付録A.4.3を参照してください。
自己遮蔽因子は(ちょうどFUELキーワードとして同位体定義を使用しています)SSFFUELまたは(質量%の自然の要素を採用)SSFMASSのいずれかの使用を介して適用されています。特定の希釈値はSSFDILUTIONキーワードを用いて手で上書きされることがあります。これらの機能の使用に関する詳細は、マニュアルの入力セクションに記載されています。
ジオメトリ自己シールド
FISPACT-IIは、直接シミュレートされたシナリオの形状を考慮していないポイントソリューションのコードですが、いくつかの堅牢な系統は、このような点光源の用量および空間的自己遮蔽などの幾何学的効果の治療のために存在します。キーワードSSFGEOMETRYは、ユーザーが空間的自己遮蔽効果のための良好な一致を与えるために箔、ワイヤ、球や円柱のために実証されている「ユニバーサル曲線モデル」を採用することができます。これらは、普遍的な無次元パラメータを使用して、純粋なターゲットに1つの共振を考えます
$$ z = \Sigma_{tot}(E_{res}) L_{eff} \sqrt{\frac{\Gamma_\gamma}{\Gamma}}, $$
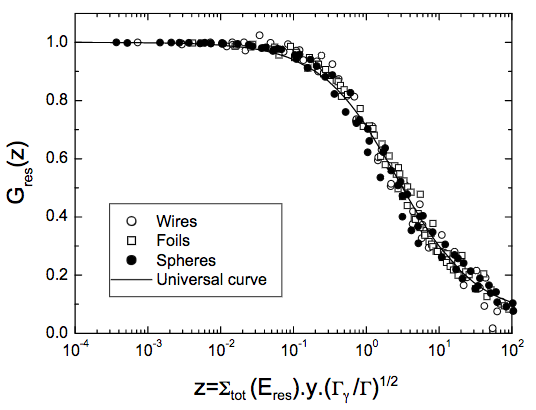
ワイヤ、箔及び球形状の値を示したの$のz $に対する共鳴自己遮蔽因子のユニバーサルカーブ。 E. Martinho et al. から撮影。
共鳴$\Sigma_{tot}(E_{res})$、「有効長」$\Gamma_\gamma$、放射性捕獲幅$L_{eff}$と総共鳴幅$\Gamma$のエネルギーで巨視的断面積に基づいて。この共振用の自己遮蔽因子は、その後、実験定数を持つ唯一の$z$の関数です。
モデルは、重み自己遮蔽因子の加重和をとることにより分離共鳴のグループに拡張されています
$$w_i = \left( \frac{\Gamma_\gamma \Gamma_n}{E^2_{res} \Gamma} \times \frac{2J+1}{2(2I+1)} \right)_i , $$
$ \ Gamma_n $は中性子散乱幅である、$ I $と$ J $はそれぞれ、ターゲットおよび化合物の共鳴状態のスピンです。 FISPACT-IIはPRINTLIBキーワードを使用して、すべての断面のための自己遮蔽因子を提供し、ターゲット材料内のすべての核種のためのグループ単位でこれらを使用することができます。
