Self-shielding is an essential aspect of calculating reaction rates which can have very strong effects on numerous observables from criticality to activation. There are two general types of self-shielding which are often classified as energy and spatial self shielding. Methods for correcting reaction rates for both of these self-shielding issues have been implemented within FISPACT-II.
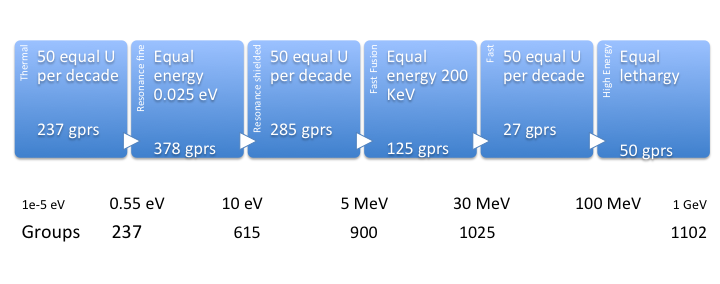
The essential feature of energy self shielding is that cross sections often contain resonances which are defined for very specific energy regions, which often have large contributions toward the total reaction rate. The large resonance will cause a depression in the neutron population around that energy which may not be reflected in simulations where this feedback is not fully taken into account. It is particularly problematic where cross sections and particle spectra are discretised into some multi-group where the depression in the population for a specific energy cannot be resolved. Since FISPACT-II requires multi-group incident-particle spectra as an input, self-shielding is essential. To minimise these effects, use of one of the UKAEA energy group structures, such as the 1102-group for incident neutrons, reduces the effects for giant resonances in the sub-10 eV energy range while the 50 equal-lethargy structure covers all other general-purpose applications.
The UKAEA-1102 energy group structure employs a mixture of 50 equal-lethargy (logarithm) per decade and fine equal-energy bins to cover general-purpose applications with self-shielding. Figures show the definition of the structure and representations as cumulative bin numbmers, lethargy widths and energy widths. For comparison the CASMO-586 and TART-660 (equal lethargy) group structures are shown as well.
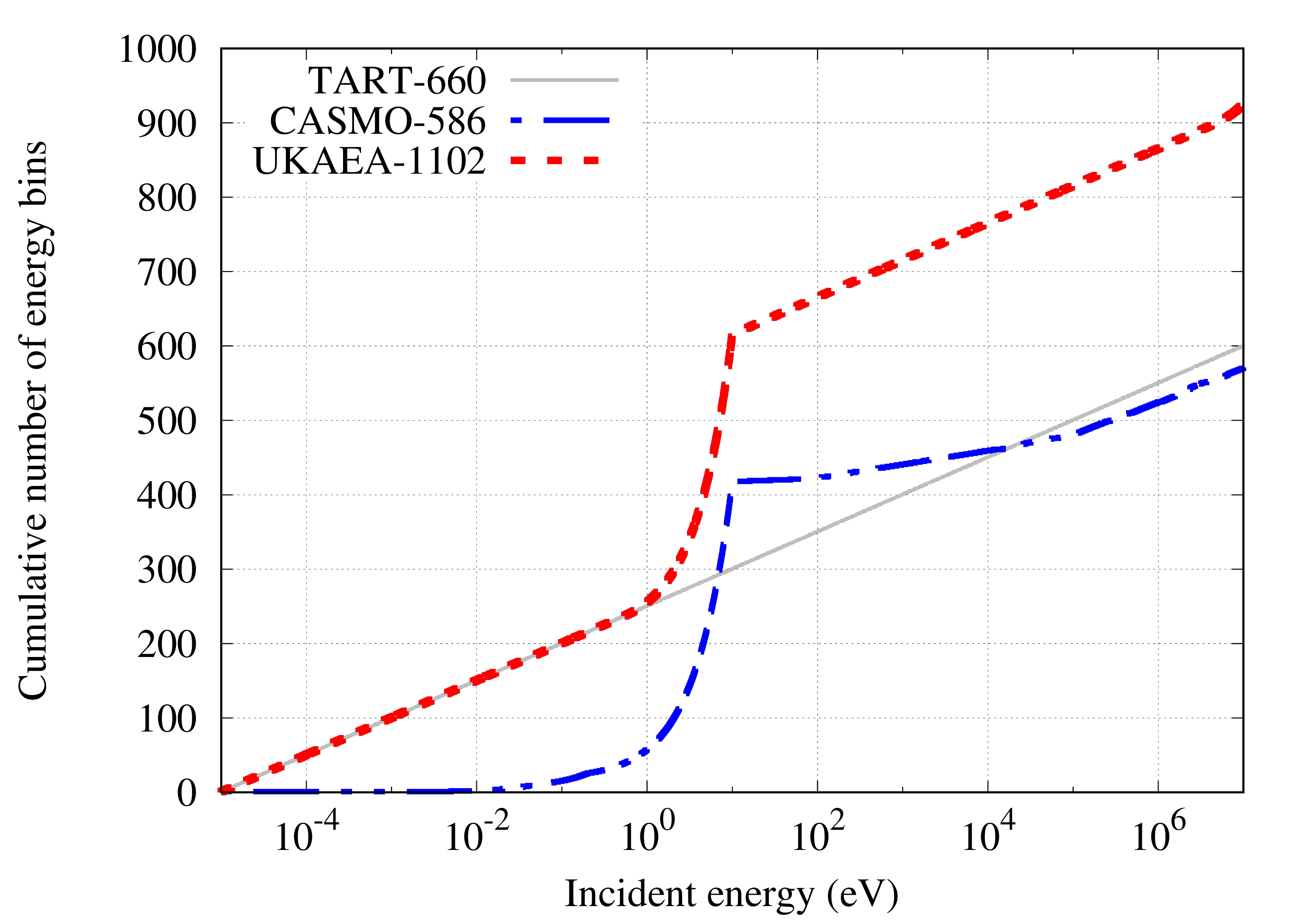
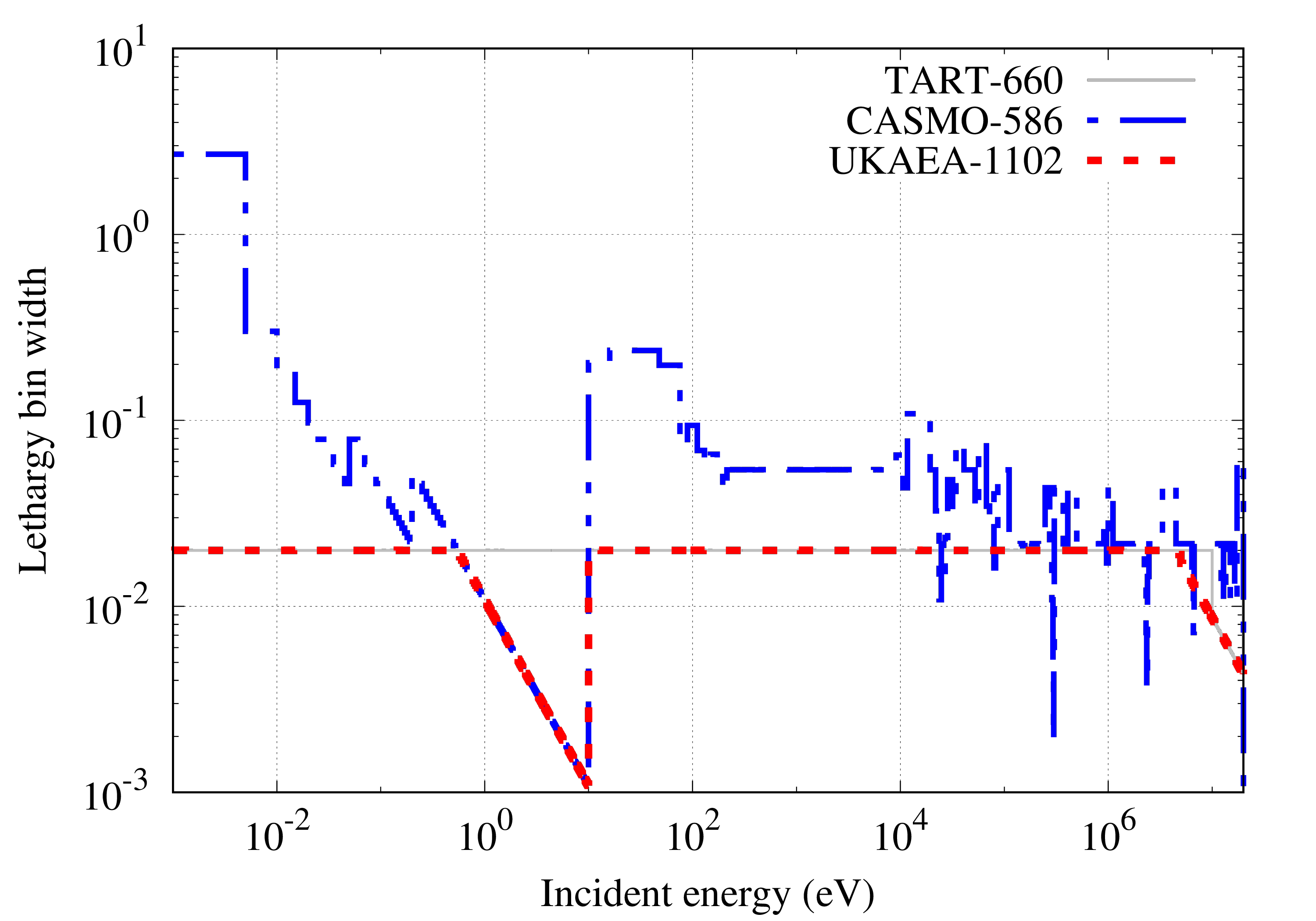
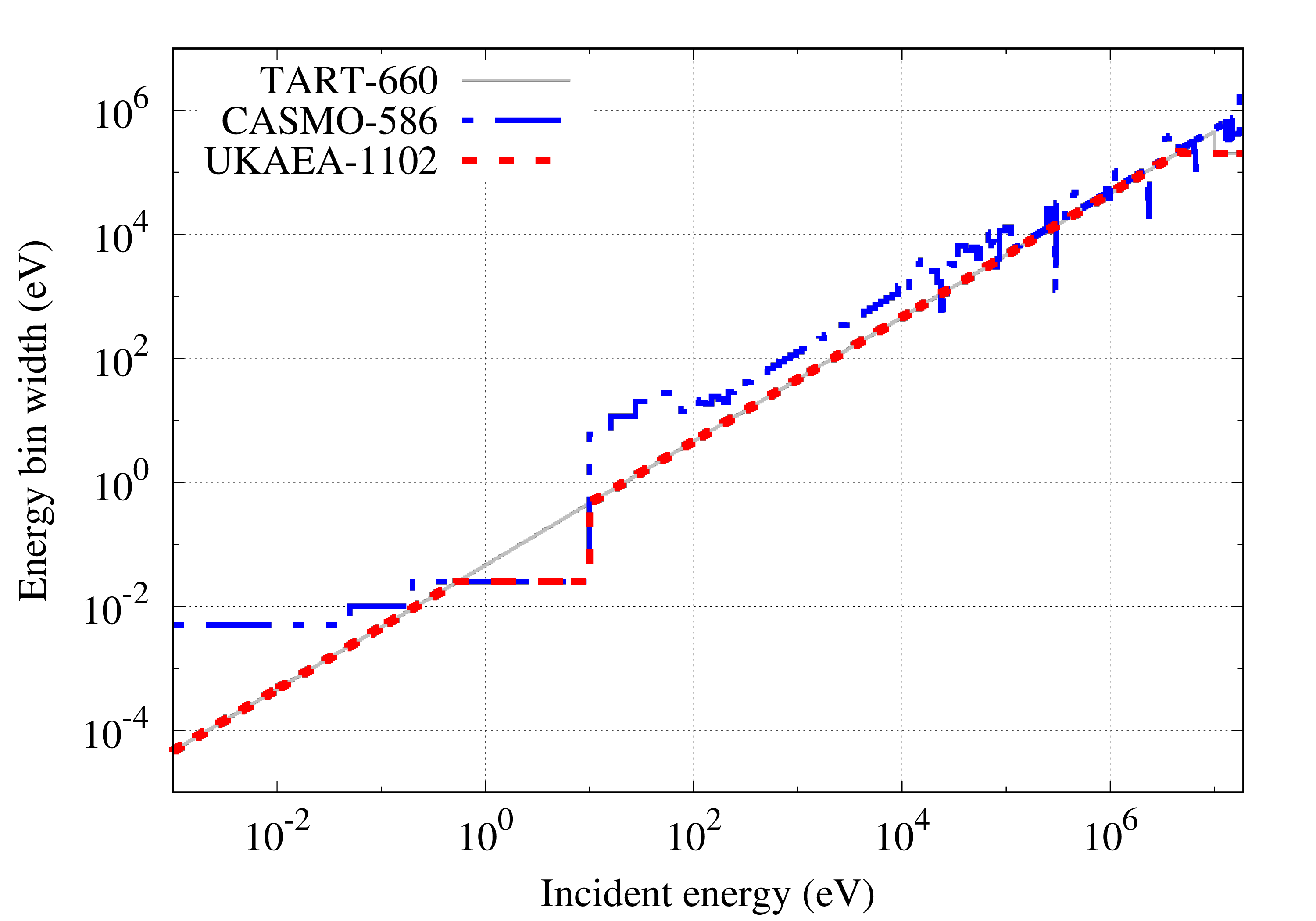
Energy-dependent self shielding
FISPACT-II employs probability tables generated by CALENDF-2010 to offer material and dilution specific reaction rates. Probability tables are provided for macro-partial cross sections including elastic scattering, absorption, fission, inelastic scattering and neutron production (excluding fission). An infinite dilution cross section is calculated based on the raw spectrum and cross sections, which may be expanded in Gauss quadratures:
$$\sigma(x,d=\infty) = \frac{1}{E_{max}-E_{min}}\int_{E_{min}}^{E_{max}} \sigma(E)\, dE = \sum_{n=1}^N P(x,n) \sigma(x,n). $$
The cross sections $\sigma$ and probability tables $P$ are dependent upon the parent nuclide $p$, energy group $g$, macro-partial index $x$ and quadrature index $n$. When a nuclide is a constituent of a homogeneous mixture, the effective cross sections in the resonance regions are reduced and can be parameterised using the dilution:
$$\sigma(x,d) =\frac{\sum_{n=1}^N P(x,n) \sigma(x,n)/(\sigma_{t}(n)+d)}
{\sum_{n=1}^N P(x,n) /(\sigma_{t}(n)+d)} . $$
Dilutions are calculated based on the material composition and an iterative algorithm using the library cross section values. These dilutions are used to recalculate the cross sections for each macro-partial. Two different approaches which are available through the PROBTABLE keyword, are to scale the reaction rates base don the total cross section or macro-partials, which also initiates different dilution algorithms. For more details see Appendix A.4.3 of the user manual.
The self-shielding factors are applied through the use of either SSFFUEL (which uses isotopic definitions just as the FUEL keyword) or SSFMASS (which employs natural elements by mass %). Specific dilution values may be overwritten by hand using the SSFDILUTION keyword. More details on the use of these functionalities can be found in the inputs section of the manual.
The self-shielding factors can be recalculated for each stage of the evolution of the nuclide inventory, shifting for example as the fuel composition of a fission reactor evolves over dozens of GWd/THM with plutonium, minor actinide and fission product build-up.
Spatial/geometry self shielding
Spatial self-shielding deals with the fact that neutron flux and local spectra can be significantly changed over short distances. In cases with strong resonances, the change in the particle spectrum over short distances can be very large in the region around the resonance. FISPACT-II is a point solution code which does not directly consider the geometry of a simulated scenario, but several robust systematics exist for the treatment of geometry effects such as point-source doses and spatial self shielding. The keyword SSFGEOMETRY allows the user to employ the universal sigmoid curve model which has been demonstrated for foils, wires, spheres and cylinders to give good agreement for spatial self shielding effects. These consider one resonance in a pure target, using a universal dimensionless parameter,
$$ z = \Sigma_{tot}(E_{res}) L_{eff} \sqrt{\frac{\Gamma_\gamma}{\Gamma}}, $$

Universal curve of the resonance self shielding factors against $z$ showing values for wires, foils and sphere geometries. Taken from E. Martinho et al.
based on macroscopic cross section at the energy of the resonance $\Sigma_{tot}(E_{res})$, ‘effective length’ $L_{eff}$, radiative capture width $\Gamma_\gamma$ and total resonance width $\Gamma$. The self-shielding factor for this resonance is then a function only of $z$ with empirical constants.
The model has been extended to a group of separated resonances by taking a weighted sum of the self-shielding factors with weights
$$w_i = \left( \frac{\Gamma_\gamma \Gamma_n}{E^2_{res} \Gamma} \times \frac{2J+1}{2(2I+1)} \right)_i , $$
where $\Gamma_n$ is the neutron scattering width, $I$ and $J$ are the spins of the target and compound resonance states, respectively. FISPACT-II can use these on a group-by-group basis for all nuclides within the target material, providing the self shielding factors for all cross sections using the PRINTLIB 6 keyword.
